Axioma: Na matemática é uma hipótese inicial de qual outros enunciados são logicamente derivados. Pode ser uma sentença, uma proposição, um enunciado ou uma regra que permite a construção de um sistema formal.
http://pt.wikiversity.org/wiki/%C3%81lgebra_linear/%C3%8Dndice/Axiomas_e_exemplos
Teorema: Consiste em
apenas uma implicação que pode ser provada.
http://penta.ufrgs.br/edu/telelab/mundo_mat/malice1/exemplo.htm#ex1
5- No filme, qual o objetivo do estudante ao treinar tênis com as marcações na parade?
Que a força que ele exercia fazia com que a bola batisse ee voltava para a direção que ele tanto queria
6- Séries lógicas... O que são ? Exemplifique
É uma ciência de índole matemática e fortemente ligada à Filosofia. Já que o pensamento é a manifestação do conhecimento, e que o conhecimento busca a verdade, é preciso estabelecer algumas regras para que essa meta possa ser atingida. Assim, a lógica é o ramo da filosofia que cuida das regras do bem pensar, ou do pensar correto, sendo, portanto, um
instrumento do pensar. A aprendizagem da lógica não constitui um fim em si. Ela só tem sentido enquanto meio de garantir que nosso pensamento proceda corretamente a fim de chegar a conhecimentos verdadeiros. Podemos, então, dizer que a lógica trata dos argumentos, isto é, das conclusões a que chegamos através da apresentação de evidências que a sustentam. O principal organizador da lógica clássica foi Aristóteles, com sua obra chamada Organon. Ele divide a lógica em
formal e
material.
7- Pesquise três diferentes sequências e mostre dois jeitos diferentes de resolver uma delas.
Anexando dois quadrados com lado=1, teremos um retângulo 2x1, sendo o lado maior igual à soma dos lados dos quadrados anteriores. Anexamos agora outro quadrado com lado=2 (o maior lado do retângulo 2x1) e teremos um retângulo 3x2. Continuamos a anexar quadrados com lados iguais ao maior dos comprimentos dos retângulos obtidos no passo anterior. A sequência dos lados dos próximos quadrados é: 3,5,8,13,... que é a sequência de Fibonacci.
Ao examinar o Triângulo Chinês (nosso conhecido Triângulo de Pascal) dos anos 1300, Fibonacci observou que esta sequência numérica aparecia naquele documento. O aparecimento se dava através da soma de vários números binomiais localizados acima e ao lado direito do número anterior.
Quando temos um segmento de reta com extremidades A e B, podemos determinar um ponto D neste segmento, dividindo-o em média e extrema razão.
8- Escreva, em poucas linhas, a sua opinião crítica sobre o filme.
Achamos o filme dinamico, as tramas foram bem boladas; exeto a obsseção do garoto ao professor.

 e
e 
 , por exemplo. Observe também que
, por exemplo. Observe também que  , veja notação de somatório
, veja notação de somatório


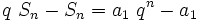
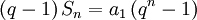
 e o resultado segue.
e o resultado segue.
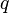 . Esta constante
. Esta constante 


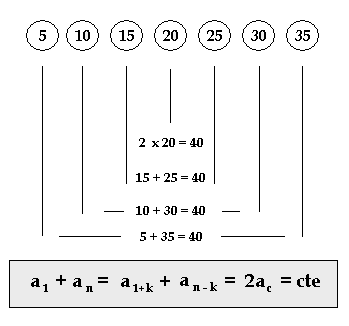
 . O número
. O número  , em que r=3(por que o numero do r é a diferença entre os numeros que vão crescendo)\,\!.
, em que r=3(por que o numero do r é a diferença entre os numeros que vão crescendo)\,\!. , em que
, em que  .
.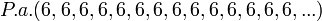 , onde
, onde 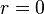 .
.